De la pensée concrète à la pensée formelle (II)
[Vers: Cours n. 12 — Cours n. 10 — Cours n. 9 — Cours n. 8 — Cours n. 7 — Cours n. 6 — Cours n. 5 — Cours n. 4 — Cours n. 3 — Cours n. 2 — Cours n. 1]
Préambule
La série de recherches examinée dans le précédent cours nous a livrés un premier aperçu de la transformation de la pensée lors du passage de l’enfance à l’adolescence, et en particulier d’une transformation des conduites expérimentales qui se manifeste en tout premier lieu par l’apparition de la méthode de dissociation permettant de découvrir les facteurs causaux déterminant un phénomène ou, à l’opposé, d’exclure des facteurs non pertinents. Mais d’autres manifestations comportementales apparaissent également à partir de 10-11 ans, qui révèlent des compétences et des structures opératoires nouvelles, lesquelles sont la raison profonde des modifications de la pensée logique et expérimentale observées chez l’adolescent. La pensée combinatoire est l’une de ces compétences et c’est par elle que nous allons d’abord poursuivre notre examen du développement intellectuel de la pensée, c’est-à-dire du passage de la logique de l’enfant à la logique de l’adolescent, avant d’aborder le chapitre des modifications structurales les plus profondes, illustrées par la genèse du groupe INRC (lequel réunit les deux formes de réversibilité, l’une, l’inversion, liée aux groupements de classe et leurs correspondants sur le plan infralogique, l’autre, la réciprocité, liée aux groupements de relations). En chemin, nous découvrirons également d’autres caractéristiques générales frappantes de la pensée adolescente, notamment son caractère hypothético-déductif et, lié à celui-ci, la façon dont la pensée formelle renverse le rapport entre le réel et le possible tel que le concevait et continue d’ailleurs en général à le concevoir la forme de pensée concrète chez tout individu ayant acquis les compétences propres à la pensée hypothético-déductive [1].
I. La pensée combinatoire
Les opérations combinatoires peuvent être décrites, en première approximation, comme la capacité de trouver ou de construire de manière systématique et ordonnée toutes les combinaisons possibles entre n éléments (par exemple des objets extérieurs ainsi que les propositions au moyen desquelles ces objets sont décrits par la pensée). Il existe différentes manières de procéder à de telles combinaisons, par exemple selon que l’on tienne compte ou non de l’ordre dans lequel les éléments sont combinés, ou encore selon que chacune des combinaisons que l’on produit contienne ou non le même nombre d’éléments que l’ensemble des éléments donnés au départ (combinaisons 2 à 2, ou 3 à 3, ou 4 à 4, ou n à n des éléments d’une collection de n éléments). Tout ceci s’éclairera à travers les quelques exemples de recherche que nous allons tout de suite présenter. Mais il convient d’emblée de souligner le rôle crucial de l’acquisition des opérations combinatoires dans le passage de la pensée concrète à la pensée formelle, ainsi que le montreront ces exemples. En l’absence de ces opérations, il ne saurait y avoir de pensée hypothético-déductive.
Venons-en aux faits. Les opérations combinatoires ont été étudiées par Piaget et Inhelder dans deux contextes : les études sur la psychogenèse de la notion de hasard, [2] et dans le cadre des recherches sur le développement des conduites expérimentales et de la logique des propositions chez l’enfant et l’adolescent, dont l’une d’entre elle avait pour objet la combinaison de corps chimiques. Avant de présenter cette dernière recherche sur les combinaisons chimiques, arrêtons-nous brièvement sur le rôle de la pensée combinatoire dans la genèse et la maîtrise du hasard.
(1) La pensée combinatoire et la genèse de l’idée de hasard
On connaît les jeux de dés dans lesquels le hasard est le seul facteur explicatif des résultats obtenus lors des lancés simultanés ou successifs (pour autant bien sûr que ceux-ci ne soient pas truqués). Supposons donc que l’on ait deux dés qu’on lance simultanément. Quelle est la probabilité d’atteindre le maximum de 12 points (6 pour chacun des dés) ? Pour connaître cette probabilité, il faut connaître non seulement le nombre de combinaisons permettant d’atteindre la somme espérée (en l’occurrence, une seule combinaison, celle de 6 et 6), mais également le nombre de toutes les configurations possibles, dans cet exemple, 6×6=36 (soit 11, 12, 13, …, 16, 21, 22, …, 26, …, …, 61, 62, …66 : chacune des 6 faces du premier dé a 6 possibilités de se combiner avec les faces du second dé). La probabilité d’obtenir la combinaison (6,6) est donc de 1/36.
On voit donc, sur cet exemple des plus simples, comment la pensée combinatoire intervient dans la capacité de penser opératoirement le hasard.
Parmi les problèmes qui ont été posés aux sujets pour étudier le développement des opérations combinatoires, il y a celui des couples que l’enfant ou l’adolescent peut construire à partir d’un tas de jetons blancs, d’un deuxième de jetons rouges, d’un autre de jetons d’une troisième couleur, etc. (le nombre de tas peut être plus ou moins grand selon le niveau de développement déjà atteint par le sujet interrogé — niveau évalué dès les premiers échanges). Les jetons (ou des poupées) sont présentés aux plus jeunes enfants comme des personnes qui se promènent deux par deux, et en principe il est précisé que les éléments composant chaque couple devraient être de couleur différente. De plus, l’ordre des couleurs à l’intérieur des couples ne compte pas (ce qui réduit le nombre des combinaisons possibles). Voilà quelques exemples de comportement qui illustrent les trois étapes franchies par la pensée combinatoire pour résoudre ce type de problèmes.
Stade préopératoire (de 4 à 7 ans environ[3]). — L’expérimentateur E demande à Lev[4] (4;8) de lui montrer toutes les façons de mettre par couple des poupées habillées soit en rouge R, en blanc Bc ou en bleu Bl (E illustre sa demande par un exemple de composition d’un couple). Lev place l’un à côté de l’autre une R et une Bl (soit {R,Bl}). « Et encore ? », lui demande E. Lev compose trois autres couples : {Bl,Bl}, {Bc,Bc} et {R,R}, arrivant ainsi à découvrir quatre des six combinaisons possibles (dans cet exemple, l’expérimentateur laisse l’enfant construire des couples de même couleur). E demande alors à l’enfant s’il peut encore trouver d’autres couples (de couleur) différents des quatre déjà proposés. Lev place encore {Bc,Bl}, puis, à la suite d’une nouvelle demande identique, {R,Bl}. E lui montre alors que ce couple a déjà été placé (les couples déjà composés par l’enfant restent toujours visibles). E demande à l’enfant si on peut mettre {R,Bc}, ce que celui-ci admet. Mais, alors que toutes les configurations possibles se trouvent sur la table, Lev ne sait que répondre à E lorsque celui-ci lui demande s’il est possible de faire encore autrement, ou bien si tout à déjà été mis.
Ce qu’illustre les comportements de cet enfant, c’est l’incapacité, à ce 1er stade, à composer, même par pur tâtonnement, tous les configurations possibles ({R,Bc} manque dans les solutions proposées par LEV). Au mieux, les seules associations que les enfants de ce niveau construisent avec une apparence de système sont les trois couples de couleur unique ({R,R}, {Bc,Bc} et {Bl,Bl}). Mais dès qu’il s’agit de composer tous les couples bicolores, l’enfant place certes sur la table de nouveaux couples, mais ceci sans nul esprit de système, et donc sans se préoccuper de savoir si la configuration d’un couple nouvellement placé n’est pas identique à celle d’un couple déjà composé. On retrouve donc à ce premier stade une caractéristique déjà détectée lors de l’examen de la genèse de la sériation logique : une façon de procéder par couples, sans mises en relation des uns avec les autres.
Stade opératoire concret (de 8 à 10 ans environ). — Dès un certain niveau de développement intellectuel, il est bien précisé aux sujets que chacun des couples composés doit être composés de deux éléments de couleur différente. Ainsi, pour trois couleurs, on a ((3×3)–3)/2 = 3, pour quatre couleurs, ((4×4)–4)/2 = 6, et pour n couleurs : ((n×n)–n)/2 possibilités différentes[5].
Dans les exemples que l’on trouve dans l’ouvrage sur la genèse du hasard, ce n’est pas avant 8 ans que les enfants (interrogés à Genève vers 1950) parviennent à trouver empiriquement les couples de jetons bicolores, et encore avec l’aide de l’expérimentateur-psychologue lorsqu’il subsiste des couples non encore identifiés. Et lorsqu’à la fin E demande s’il n’y a pas un truc pour être sûr de découvrir toutes les manières de faire, ces enfants ne peuvent trouver autre chose que la simple répétition de la démarche empirique qui les a conduits à découvrir l’ensemble des configurations possibles de couples bicolores.
Donnons un exemple d’un comportement de ce niveau. Fre (8;6), pour 4 couleurs A, B, C et D, trouve empiriquement les 6 combinaisons possibles (AB, AC, AD, BC, BD et CD). Avec un plus grand nombre de couleurs, il parvient à trouver un certain nombre de combinaisons supplémentaires, mais c’est seulement avec une certaine aide de E qu’il les obtient toutes. [6]
En un mot, la maîtrise des opérations de classification et de sériation propres à la pensée opératoire concrète ne suffit pas à découvrir un système général permettant aux enfants de ce niveau de découvrir l’ensemble des combinaisons possibles, quel que soit le nombre de couleurs à combiner. Dès que l’on dépasse les situations les plus simples, enfants ne manquent pas de rechercher et d’utiliser des procédés apportant un début de système, mais qui ne valent que pour certains couples (par exemple, le procédé de commencer par poser des couples au moyen d’un seul jeton pris successivement dans chaque tas —c’est le cas par ex. pour Dan[7] (9;6) qui pose AB et CD, puis les couples restants tels que BC et AD, et ensuite AC et BD)—, mais sans que les procédés localement utilisés puissent engendrer de manière systématique l’ensemble des couples possibles quel que soit le nombre de couleurs (Dan n’est parvenu à trouver le reste des couples restants pour 4 couleurs que parce que ces derniers sont peu nombreux).
Stade opératoire formel. — Vers 11-12 ans les sujets parviennent à trouver immédiatement (pour les plus avancés), ou après quelques essais (pour les moins avancés) le procédé systématique leur permettant de trouver l’ensemble des couples que l’on peut composer avec des jetons de 6 couleurs différentes. C’est par exemple le cas de Lau[8] (12;3) qui procède comme suit. Il pose 5A (=jaune) en verticale et leur associe les 5 autres couleurs B, C, D, E et F, puis il pose 5B [= bleus] dans une colonne parallèle et leur associe C, D, E et F ; puis, s’apprêtant à mettre un A, il se corrige en disant : « Non, puisque je l’ai [= le bleu] déjà mis avec le jaune ». Il commence une nouvelle colonne, cette fois de 4C, auxquels il associe D, E et F, puis retire le quatrième C en affirmant : « Ah, ça diminue chaque fois de un ». Le procédé déjà systématique utilisé au départ, est très vite corrigé pour déboucher sur une manière de faire qui permettra par la suite de trouver tous les couples possibles.
S’il faut attendre les débuts du stade de la pensée formelle pour découvrir de tels procédés, c’est que, contrairement par exemple à la mise en correspondance de deux sériations indépendantes (par exemple des cannes de différentes hauteurs pour des personnages de plus en plus grands) qu’un enfant du stade des opérations concrètes effectue sans difficulté, dans un système combinatoire, chaque étape de mise en ordre dépend dans son organisation de l’ordre établi à l’étape précédente. Dans l’exemple de Lau exposé ci-dessus, la construction de la colonne 2 est en partie déterminée par les combinaisons réalisées pour la colonne 1, idem pour la colonne 3 par rapport aux colonnes précédentes, et ainsi de suite. C’est donc non plus seulement une correspondance entre sériations qui est nécessaire pour résoudre opératoirement le problème de combinatoire, mais une sériation de sériations, donc une opération (supérieure) sur des opérations qui, dans leur composition, dépendent donc des potentialités propres à l’opération supérieure. En un mot, ce qui est engendré par cette combinaison supérieure d’opérations de niveau concret, c’est un véritable système de systèmes, et c’est précisément cette capacité de combiner des opérations de niveau inférieur (et obéissant elles-mêmes déjà à des lois de groupement ou de groupe) que l’on va découvrir à l’œuvre, de manière plus ou moins visible, dans les conduites des adolescents confrontés aux problèmes créés dans le cadre des recherches d’Inhelder et Piaget sur la genèse de la logique des propositions (ou plus précisément sur le genèse des opérations interpropositionnelles). Cette capacité propre à la pensée combinatoire de sérier des sériations, ou encore de les classer, donc à opérer sur des opérations concrètes et non plus seulement sur des objets est en effet la clé de résolution non seulement des problèmes artificiellement et explicitement combinatoires, comme celui que l’on vient d’illustrer, mais de ceux qui exigent des combinaisons causales, comme on va le constater tout de suite dans le cas de la combinaison de substances chimiques, ou encore de ceux liés aux combinaisons propres aux opérations interpropositionnelles, comme on le verra un peu plus loin.
(2) Les combinaisons de corps chimiques
Les quelques faits dont il va être question sont exposés et analysés dans le chapitre vii de l’ouvrage de 1955 sur le passage de la logique de l’enfant à la logique de l’adolescent.[9] Cette recherche qui avait pour objet l’examen des conduites de sujets confrontés à un problème de combinaison de corps chimiques a été réalisée en collaboration avec Gérald Nœlting, qui, après un doctorat en chimie, s’était tourné vers la psychologie et l’épistémologie génétiques.
Voilà le type de problème de combinaison chimique auquel sont confrontés des enfants et adolescents âgés de 5 ans à 15 ans. Soit des récipients (quatre ou cinq selon les niveaux de difficulté du problème adaptés aux niveaux de compréhension possible des sujets interrogés) dont un ou deux peuvent contenir de l’eau pure, deux ou trois autres des liquides incolores autres que de l’eau pure lesquels, une fois mélangés, peuvent produire (pour l’une des combinaisons) de la couleur, et enfin une solution (= un mélange liquide incolore) qui au contraire fait disparaître la couleur ou l’empêche d’apparaître. Le type de problème que les sujets vont devoir résoudre sera de trouver l’effet des différentes combinaisons possibles. Notons encore que des signes distinctifs sont marqués sur les récipients, ceci afin de bien distinguer la provenance des différents liquides incolores utilisés lors d’une combinaison (ces signes sont par exemple des chiffres : I pour le premier récipient, II pour le deuxième, etc.). L’expérimentateur-psychologue E commence par réaliser lui-même la combinaison produisant un mélange coloré, mais sans bien sûr que l’enfant puisse mémoriser les récipients utilisés à cet effet (pour les sujets les plus âgés, il suffit de leur dire qu’il est possible de faire surgir un liquide coloré en mélangeant les liquides provenant de différents récipients). Après cette démonstration ou cette indication, E demande au sujet de mélanger à son tour les liquides de manière à faire apparaître une solution colorée.
Voilà quelques exemples de comportement qui illustrent les étapes franchies par la pensée combinatoire pour résoudre ce type de problèmes.
Stade I (niveau préopératoire). — À ce niveau, les enfants se contentent le plus souvent d’associer les liquides de deux (rarement trois) récipients pris au hasard, puis à nouveaux deux autres, etc. en se contentant de décrire les résultats et à livrer des explications phénoménistes (basées sur le seul constat de coprésence perceptive[10]) ou prélogiques[11], par exemple liées à de supposées propriétés de la couleur, mais non pas à la possible action d’une substance sur une autre. Ainsi, Nod[12] (5;5) parvient par hasard à faire apparaître du « sirop » (= un liquide rose) en combinant les deux liquides incolores (l’un composé d’eau et soude caustique, l’autre composé d’eau et de phénolphtaléine) qui, mélangé, produisent effectivement de la couleur. A l’expérimentateur qui lui demande s’il peut à nouveau faire du sirop, il répond affirmativement en mélangeant les mêmes liquides, et il explique que pour faire surgir la couleur, « il faut faire comme ça » (= secouer le récipient qui contient de l’eau). Puis il prend à nouveau le liquide contenant du phénolphtaléine qu’il mélange avec une solution d’acide sulfurique. Cette fois, le mélange est incolore, « de l’eau » dit l’enfant, parce que, selon lui, qui répond à une question de l’expérimentateur, le sirop est parti dans un autre récipient (une bouteille se trouvant à un mètre de distance !). Un autre enfant, Eg(6;6) affirmera que l’eau devient rose parce que « peut-être il y a de la peinture » dans le verre où les deux liquides incolores ont été mélangés. Etc.
En conclusion, les enfants de ce premier stade n’essaient à aucun moment d’introduire un minimum d’ordre dans leurs actions successives, et ils n’ont pas l’idée que le mélange en tant que tel soit la cause de l’apparition de la couleur. Voyons donc ce qu’il en est des enfants de niveau opératoire.
Stade des opérations concrètes. — Entre 7 et 10-11 ans environ, les enfants peuvent utiliser l’opération de sériation ou encore l’opération de multiplication logique (au moyen de laquelle ils peuvent concevoir un composé comme le produit de deux ou plusieurs éléments) pour commencer à mélanger avec système un premier liquide avec les autres, puis un second avec tous les autres ou seulement quelques autres, mais sans pouvoir se faire une vision d’ensemble des combinaisons possibles, ou plus précisément sans pouvoir coordonner ces esquisses de systématisations successives pour aboutir à un système d’ensemble permettant de prévoir la totalité des combinaisons possibles. C’est donc par des tâtonnements partiellement dirigés que ces enfants réussissent à atteindre le but fixé (obtenir un mélange coloré). Par ailleurs, contrairement aux enfants de niveau préopératoire, ils comprennent bien que c’est le mélange de certains liquides qui peut faire surgir la couleur, ou en certains cas, la faire disparaître. Illustrons par trois exemples les comportements typiques des enfants ayant atteint le niveau des opérations concrètes.[13]
Exemple 1 : Im[14] (7;6, stade IIA) a devant lui les quatre flacons numérotés 1 (acide sulfurique), 2 (eau), 3 (eau oxygénée) et 4 (thiosulfate), ainsi qu’une bouteille compte-goutte étiquetée g et qui contient de l’iodure de potassium. Combiné avec l’eau oxygénée (3) et l’acide sulfurique (1), g produit un mélange de couleur jaune. Par contre, il suffit de verser une solution de thiosulfate (4) dans le mélange coloré pour que la couleur disparaisse. Isolés, les cinq liquides sont bien sûr incolores. Il s’agit d’obtenir la couleur jaune (produite par le mélange 1x3xg) et, une fois atteint ce résultat, d’expliquer ce qui entraîne l’apparition de la couleur, ou au contraire sa disparition ou son absence. L’enfant a à sa disposition pour ses essais de mélange un grand nombre de verres vides, tous de même taille et de même forme.
Im commence par mélanger dans quatre de ces verres des solutions provenant du compte-goutte g avec les solutions provenant des quatre autres récipients, en obtenant ainsi les combinaisons : 4g, 3g, 2g et 1g. Comme rien ne se passe, il commence par ajouter sans succès de nouvelles gouttes g à 3g, puis aux trois autres combinaisons. Devant l’absence de résultat, il mélange dans l’ordre 3×2×1×4, en mettant à chaque fois quelques gouttes g, ce qui s’est traduit par l’apparition de la couleur après 3g×2g×1g, puis disparition de la couleur dès l’ajout de 4. À la question de savoir pourquoi la couleur a pu disparaître, l’enfant répond qu’il a trop mis de liquide. Au début des opérations concrètes, l’enfant reste donc démuni face à un tel problème, quand bien même il sait que pour atteindre son but, il faut mélanger les liquides, donc procéder à des multiplications logiques, mais sans pour autant parvenir à dissocier ni à démontrer le rôle de chacun des liquides, exception faite de celui qui fait disparaître la couleur. Il ne lui vient pas du tout à l’esprit de procéder 2 à 2, puis 3 à 3, etc., contrairement à ses camarades plus avancés dans le développement et l’usage des opérations concrètes.
Exemple 2 : Alb[15] (10;4, stade IIB) commence par tout mélanger dans l’ordre 1×2×3×4×g, ce qui ne fait pas apparaître la couleur. Après quoi il recommence, mais en modifant l’ordre (3×1×4×2×g), ce qui aboutit à nouveau à un échec. Comme le mélange reste incolore, il procède à quelques essais supplémentaires, qui tous sont infructeux et le conduisent à abandonner toute nouvelle tentative. À E qui, face au découragement de l’enfant, lui demande s’il est nécessaire de prendre du liquide de tous les flacons, il dit que l’on peut en prendre 2 ou 3 à la fois. Il essaie et tombe juste par hasard, ce qui le satisfait.
Contrairement à son camarade un peu plus jeune, Alb introduit donc un début de systématique en essayant plusieurs permutations des cinq liquides toujours pris tous ensemble. Mais si l’appui que lui donne E l’ouvre à de nouvelles solutions possibles, il ne dispose pas lui non plus des opérations qui lui permettraient d’engendrer et d’explorer toutes les possibilités. Voyons enfin un dernier exemple qui illustre les progrès possibles dans l’utilisation des opérations concrètes dans un tel problème de combinatoire.
Exemple 3 : Tur[16] (10;4, stade IIB) procède par étapes successives, en utilisant des règles locales. Il commence en mélangeant chacun des quatre liquides avec quelques gouttes de g : 1×g, 2×g, 3×g, 4×g. Comme cela n’a abouti à rien, il décide de mélanger les quatre liquides en ajoutant un peu de g : 1×2×3×4×g. En l’absence de coloration, il essaie 1×4×g, 2×3×g, 3×4×g, et 2×1×g, mais sans épuiser toutes les possibilités (il manque en particulier l’une des deux combinaisons produisant la couleur : 1×3×g). Ensuite il passe spontanément aux combinaisons par trois (avec chaque fois un peu de g), mais là encore sans une procédure systématique permettant d’explorer la totalité des combinaisons par ordre. Toutefois, son exploration empirique le conduit cette fois à engendrer toutes les combinaisons 3 à 3 (avec toujours en plus et à chaque fois un peu de g), et en particulier la combinaison 3×2×1g, dont il constate qu’elle fait apparaître la couleur (rappelons que 2 est de l’eau pure ; raison pour laquelle il aurait pu aboutir plus vite à une solution s’il n’avait pas omis la combinaison 1×3g, ou 3×1g, l’ordre étant indifférent). Et de ce succès (faute d’avoir exploré toutes les combinaisons), il croit pouvoir conclure que les trois liquides 3, 2 et 1 sont nécessaires. Seules les questions de E le conduiront à découvrir l’existence de la deuxième solution (le mélange 3×1×g). Et finalement, lorsque E lui demande de résumer l’effet des quatre liquides 1,2,3 et 4, il se trompe en affirmant que le 4 ne fait rien, et en attribuant au 3 l’effet de supprimer la couleur (ceci peut-être en ayant en vue le fait qu’au début, lorsque les cinq liquides, y compris g, ont été tous mélangés ensemble, la couleur n’est pas apparue).
Ces différents exemples suffisent à montrer que les capacités de sériation, de mise en correspondance, de multiplication logique, etc., propres à la pensée opératoire concrète ne suffisent pas à amener les sujets à découvrir les procédés combinatoires seuls aptes à organiser leurs actions de manière à produire l’ensemble des combinaisons possibles et du même coup à découvrir les raisons de leurs réussites ou de leurs échecs face à ce problème de mélange des liquides (par attribution déductivement et non pas seulement empiriquement fondée du rôle que jouent les différents liquides lors du mélange). Comme on va le voir, les comportements des sujets changent radicalement dès qu’ils accèdent à la pensée combinatoire [17], composante essentielle de la pensée expérimentale et hypothético-déductive.
Stade des opérations formelles. — Après éventuellemt quelques expériences destinées à prendre connaissance du matériel, à mieux saisir le problème auquel ils sont confrontés, et peut-être à tomber par hasard sur la bonne solution, les sujets parvenus au stade formel ne procèdent plus par tâtonnement mais sont systématiquement guidés dans leurs essais par un plan préalable d’action, qui peut se préciser en cours d’activité, et qui repose sur l’idée qu’il est nécessaire de tester toutes les combinaisons possibles sans en oublier aucune (sauf si à partir des constats déjà réalisés, des conclusions certaines s’imposent concernant ce que peuvent produire des combinaisons non déjà effectuées). Donnons un seul exemple de ce dernier niveau, dont on peut trouver le protocole détaillé à la page 108 de l’ouvrage de 1955. [18]
Eng (14;6) commence par émettre l’hypothèse qu’un mélange de l’un des quatre liquides 1, 2, 3 ou 4, avec quelques gouttes contenues dans g, suffit à faire venir la couleur. Après constat que cela n’est pas le cas, il sait qu’il va falloir explorer tous les mélanges possibles. Il produit d’abord les six combinaisons deux à deux, en ajoutant chaque fois quelques gouttes de g (soit : {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}), ce qui lui permet de découvrir que 1×3×g donne la couleur jaune. Puis il se demande si l’ajout de 2 ou de 4 à {1,3} ne peut pas avoir le même effet que l’ajout de g. Il constate que cela n’est pas le cas. Repartant de la composition 1×3×g, il cherche à voir ce que fait sur cette composition l’ajout de 2 ou de 4, et il découvre ainsi que l’ajout de 4 décolore 1×2×g.
Interrogé sur la Q de savoir si 1 ou 3 peuvent être de l’eau, il les remplace chacun tour à tour par ce qu’il sait être de l’eau, soit 0, pour produire une combinaison 0×3×g et une combinais. 1×0×g ; comme ces combinaisons restent incolores, il en conclut que 1 et 3 ne sont pas de l’eau.
A la fin, se remémorant les étapes de sa résolution du problème, il en déduit que 2 peut être de l’eau, que 1, 3 et g ne le sont pas et sont tous trois nécessaires pour produire la couleur, et enfin que 4 décolore la combinais. 1×3×g.
En conclusion, parvenu au stade de la pensée formelle ou hypothético-déductive, les sujets sont capables 1° de produire avec méthode l’ensemble des combinaisons permettant de tester leurs hypothèses ou de rechercher en étant certain de pouvoir le ou les trouver les combinaisons qui font surgir la couleur, et 2° de prouver, en sélectionnant les combinaisons appropriées, le rôle ou l’absence de rôle de chacun des liquides. Pour démontrer que le liquide 2 est neutre, il leur suffira ainsi de constater que son ajout à la combinaison 1×3×g ou son retrait de cette combinaison ne modifie pas l’effet de coloration obtenu en combinant 1, 3 et g.
Exprimons les pensées qui guident l’action du sujet du troisième stade, ou les justifications qu’il donne de ses sélections de liquide, au moyen des instruments de modélisation offerts par la logique symbolique. Si p symbolise la présence de la couleur et q l’ajout du liquide 2, le constat que le sujet est amené à faire est symbolisé de la manière suivante :
(p · q) ∨ (p · q) ∨ (p · q) ∨ (p · q),
ce qui, retranscrit en langage ordinaire, veut dire qu’ajouter (soit q) ou ne pas ajouter (soit q) du liquide à un mélange prélable qui a abouti (p) ou non (soit p) à faire apparaître la couleur ne change rien à la présence ou à l’absence de couleur de ce mélange (puisqu’on peut avoir p aussi bien avec q qu’avec non q, et non p aussi bien avec q qu’avec non q). Remarquons que, pour le psychologue dont l’objet d’étude est le fonctionnement de l’intelligence, l’utilité de transcrire en langage symbolique la logique du sujet en train de résoudre un problème tel que celui de la combinaison des liquides n’est pas en soi évidente. Elle s’impose au contraire lorsque, comme on va s’en apercevoir tout de suite, le même usage de la logique symbolique appliqué à des contextes dans lesquels les sujets sont invités à résoudre des problèmes différents rend visible la parenté des formes de pensée mises en œuvre par les sujets dans les différentes situations-problèmes auxquelles ils sont confrontés, et plus précisément les structures opératoires qui sous-tendent le fonctionnement de l’intelligence.
II. Le rôle du groupe INRC dans la pensée de l’adolescent
Examinons, pour terminer, les comportements et réponses des enfants et des adolescents confrontés à des épreuves opératoires qui ont pour particularité de rendre particulièrement visibles le rôle du groupe INRC dans le fonctionnement de la pensée formelle, groupe très simple, composé de quatre opérations, et qui opèrent aussi bien sur la combinatoire propositionnelle que sur les combinaisons matérielles que l’on peut faire d’éléments concrets (par exemple chimiques), mais qui sont elles aussi guidées par cette pensée.
Commençons par rappeler ce que sont les quatre opérations composant le groupe INRC et tombant donc sous ses lois de fonctionnement. I désigne tout opération (par exemple, une combinaison particulière de propositions, ou bien, comme nous l’avons vu ci-dessus, l’ajout —tel qu’il est conçu par le sujet— d’un liquide, ou encore, comme nous le verrons, d’un poids) ; N symbolise la négation de cette opération ; R l’opération réciproque, compensant toute opération I par une opération qui n’est pas sa négation ou son inverse, mais qui comme celle-ci annule ses effets) ; enfin C symbolise la négative de la réciproque et opère donc dans le même sens que I, comme des exemples le montreront dans la suite.
A noter encore que ce groupe INRC était déjà impliqué dans certaines réponses de sujets interrogés dans le cadre d’une recherche publiée en 1946 sur la psychogenèse de la notion de déplacement relatif, mais sans que Piaget ne l’ait semble-t-il alors détecté. C’est dans le cadre des travaux d’analyse et de modélisation logistique du calcul des proposition que Piaget a été amené à formuler et peut-être découvrir le rôle fondamental de ce groupe dans le fonctionnement de la pensée formelle, ce qui l’a amené à réinterpréter les résultats de sa recherche sur la notion des déplacements relatifs. Avant de présenter une expérience sur la notion de proportionnalité dans la maîtrise de laquelle le groupe INRC apparaît très clairement à la lumière des conduites observées, il est intéressant de prendre connaissance de cette recherche antérieure dans la mesure où elle nous permet de cerner avec précision le saut théorique considérable pour la psychologie génétique qu’ont été les recherches logiques de Piaget ayant aboutit à la découverte de ce groupe.
(1) Le groupe INRC et la relativité des déplacements
Voilà le problème auquel les collaborateurs de Piaget ont confronté les sujets dans le cadre des recherches sur Les notions de mouvement et de vitesse chez l’enfant (Paris, PUF, 1946). Soit un escargot Esc se déplaçant sur une planche P qui elle-même peut être déplacée de gauche à droite ou de droite à gauche relativement au sujet observant (tous les déplacements de Esc et de P se font donc exclusivement de gauche à droite ou inversement par rapport au sujet qui les observe). Dès le niveau des opérations concrètes, les sujets n’ont aucune peine à concevoir que Esc qui avance d’une certaine distance d de gauche à droite sur P alors immobile peut annuler ce déplacement (revenir à son point de départ) en effectuant un déplacement inverse d’une même longueur sur P, laquelle reste toujours immobile. Le même sujet n’aura également aucune peine à concevoir ce qui se passe si, Esc restant immobile après s’être déplacé de d cm de gauche à droite (par rapport au sujet), on déplace P d’une même distance d mais de droite à gauche : il sait que Esc se retrouvera au même point par rapport à lui qu’il l’était avant de s’être déplacé de gauche à droite. Cette fois, c’est le mouvement en sens inverse de la planche qui annule le mouvement en sens direct réalisé par Esc. Mais, et c’est là tout l’intérêt de cette expérience, il faut attendre le niveau de la pensée formelle pour que l’enfant puisse prévoir correctement ce qui se passe lorsque les déplacements de Esc et de P sont réalisés simultanément.
Présentons quelques exemples de ce qui se passe au niveau de la pensée concrète, puis au niveau de la pensée formelle [19].
Période de la pensée concrète (Piaget distingue trois sous-niveaux) — Au début de la construction et de l’utilisation opérations concrètes, Ton[20] (6;7) ne tient compte que d’un seul des deux mouvements pour indiquer où se trouve le point d’arrivée final de Esc (lorsque Esc et P avancent dans la même direction d’un distance de e et de p , seul le mouvement de P est pris en considération ; et au contraire seul celui de Esc est pris en considération si P et Esc avancent dans des directions opposées, l’un de droite à gauche, l’autre de gauche à droite, ou inversement, par rapport au sujet qui les observe).[21]
Au deuxième sous-niveau, les enfants parviennent bien à reconnaître que la planche a avancé de telle longueur, que de son côté l’escargot a avancé (ou reculé) de tant par rapport à la planche, mais ils sont incapables de composer ces mouvements (additionner plusieurs mouvements de P et de Esc effectués dans le même sens, ou, lorsque, P et Esc se déplacent en sens contraire, à soustraire le mouvement que fait la planche au mouvement que fait l’escargot lorsque tous deux se déplacent simultanément, et cela que leurs déplacements respectifs soient de même longueur ou non. Ainsi, dans le cas de deux déplacements de sens contraire, Iac[22] (7;7), qui se sert de bandes de papier pour mesurer les distances parcourues, ne fait-il que reporter, au moyen d’une telle bande, et à partir du même point de départ initial de P et de Esc, la longueur du déplacement de l’escargot sur la planche, sans donc tenir compte du déplacement réalisé par P). Et quant aux déplacements dans le même sens de Esc et de P, Iac se contente là aussi de reporter la longueur de déplacement de Esc sur P à partir de leur point de départ commun, puis, après que l’expérimentateur lui a demandé ce qu’il en est du déplacement de la planche, de reporter la longueur de ce dernier à partir de ce même point de départ (en plaçant donc la bande de papier mesurant le déplacement de P à côté et non pas dans le prolongement de la bande de papier reportant le déplacement de Esc).
Il faut attendre le troisième sous-niveau (à partir de 8-9 ans environ) de développement des opérations concrètes pour que les enfants parviennent à additionner avec exactitude les déplacements s’effectuant simultanément et dans la même direction de P et de Esc, ainsi qu’à juger que Esc ne bouge pas (par rapport au repère de départ) lorsque Esc et P font un déplacement égal mais en sens contraire. Par contre, ils ne parviennent pas à savoir où se trouvera Esc à son arrivée si les déplacements de sens contraire sont inégaux (donc à soustraire le déplacement de P au déplacement de Esc pour savoir où se trouve exactement Esc à l’arrivée, par rapport à la marque signalant le point de départ commun des deux mobiles). Dans cette dernière situation où Esc et P se déplacent en sens contraire avec des longueurs différentes, les enfants procèdent de la même façon que le faisaient les sujets du deuxième sous-niveau de la période concrète confrontés à des déplacements relatifs trop complexes pour être composés (ils ne font que rapporter le déplacement de Est à partir de son point de départ, sans tenir compte de la longueur du déplacement effectué par P, donc, en cette situation, à soustraire cette longueur au déplacement de Esc).
Niveau de la pensée formelle (à partir de 11 ans environ). — Vu la grande simplicité de cette épreuve, c’est très tôt (p. r. aux épreuves de proportionnalité dont nous allons tout de suite présenter un exemple) que le sujet de ce niveau parvient à coordonner immédiatement, en les additionnant ou en les soustrayant, les déplacements en jeu, ceci dans la mesure où il peut composer les opérations de déplacement propres à chacun des deux mobiles liés l’un à l’autre, que ces déplacements soient de même sens ou de sens contraire, et égaux ou inégaux.
Comme nous venons de l’indiquer, cette recherche a été réalisée avant la découverte du groupe INRC. Aussi, lorsqu’il analyse au milieu des années 1940 les résultats de cette enquête, Piaget en déduit-il que, hormis le fait de pouvoir traduire les opérations concrètes sur le plan verbal, « les opérations formelles n’ajoutent rien aux opérations concrètes en tant qu’opératoires : elles les traduisent simplement sur un nouveau plan, qui est celui des assomptions ou des hypothèses ». [23] Piaget conserve ainsi son explication des années 1920 selon laquelle la pensée formelle ne fait que refléter sur le plan verbal la logique des opérations concrètes, avec un décalage lorsque, comme c’était le cas dans la plupart des recherches des années 1920, il s’agissait pour les sujets de résoudre des problèmes logico-mathématiques en l’absence de tout appui concret, donc de manière verbale et avec le seul recours aux images mentales. Mais dès que, à la fin des années 1940, Piaget entreprend l’analyse algébrique approfondie de la logique des propositions —ce qui l’amène à découvrir que les structures sous-tendant celle-ci ne se réduisent pas aux structures de la logique des opérations concrètes (alors simplement reformulées sur le plan verbal)— il peut, en revenant sur ces anciens résultats, en donner une toute nouvelle interprétation précisément basée sur la découverte du groupe INRC. Cette nouvelle interprétation est exposée dans les conclusions de l’ouvrage conjointement conçu avec B. Inhelder à la suite des recherches de celle-ci sur la progression des attitudes et des conduites expérimentales, de l’enfance à l’adolescence. Voilà, de manière très résumée, et là aussi avec un minimum de symbolisation, la nouvelle interprétation à laquelle aboutit Piaget sur ce qui permet fondamentalement à des sujets, et ce dès l’âge de 11 ans environ, de résoudre des problèmes très simples de mouvements relatifs similaires à celui examiné ci-dessus.
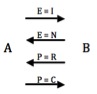Soit I un déplacement de E, soit N le déplacement en sens inverse du même mobile. Soit R un déplacement de même sens que N de la planche P (et qui, réciproque de I, annule donc également ce dernier), et enfin soit C le déplacement par laquelle la planche peut annuler son propre déplacement par un déplacement inverse (qui est alors le réciproque non pas de I mais de N). C’est le fait pour le sujet d’être guidé par cette structure opératoire composant et coordonnant les opérations appartenant aux deux systèmes d’opérations directes agissant l’un sur l’escargot, l’autre sur la planche, qui lui permet de concevoir immédiatement et sans difficulté (dans le contexte d’un problème aussi relativement simple) ce qu’il convient de faire pour connaître le déplacement que fait E effectue par rapport à son point de départ lorsque l’on tient compte du déplacement réalisé par ailleurs par P (et vice versa bien sûr).
Mais reprenons maintenant le fil des expériences sur le développement progressif des conduites expérimentales de l’enfance à l’adolescence en examinant comment interviennent la notion de proportionnalité et le groupe INRC qui la sous-tend dans la résolution d’un problème d’équilibre d’une balance à fléau (voir l’image ci-dessous).
(2) L’équilibre de la balance, la notion de proportionnalité et le groupe INRC
Cette expérience se fait au moyen d’un type particulier de balance à fléau (cf. la photographie). Les sujets sont invités à suspendre des objets des deux côtés du balancier, à déterminer les effets de ces placement, ou encore à faire en sorte d’équilibrer les deux poids de manière à ce que le balancier redevienne horizontal comme il l’était avant de suspendre des objets.
Les facteurs en jeu sont donc les poids P1 et P2 des objets O1 et O2 suspendus de chaque côté du balancier, l’augmentation ou la diminution de ces poids P1 et P2, les distances L1 et L2 de O1 et O2 par rapport au milieu (ou aux deux extrémités) du fléau, et l’augmentation ou la diminution de ces deux distances.
Pour atteindre l’équilibre horizontal du balancier, la solution la plus simple est bien sûr de choisir deux poids égaux que l’on place à des distances égales. Mais à supposer que l’on ne dispose pas parmi les objets disponibles d’un objet de poids égal à celui déjà placé sur l’un des deux côtés du fléau, et à supposer par exemple que l’on commence par prendre un objet O2 moins lourd, pour atteindre malgré tout l’équilibre, on peut soit augmenter son poids en suspendant à celui-ci un autre objet de telle sorte que leur poids total P2 soit égal à P1, soit compenser l’insuffisance de poids non pas en augmentant P2, mais en diminuant proportionnellement L1 (c’est-à-dire en rapprochant O1 de l’axe du balancier), soit encore augmenter proportionnellement la distance L2 à laquelle on suspend O2.
L’équation qui résume les rapports dans le cas de l’équilibre horizontal du balancier est simple : P1×L1 = P2×L2, ou P1/P2=L2/L1. On a donc clairement affaire ici à un problème de proportionnalité et voilà comment, dans la formalisation qu’en propose Piaget, le groupe INRC intervient dans la résolution lorsque l’on considère l’ensemble des modifications possibles de chacun des facteurs [24] :
I et N concerne les deux types d’action possibles par rapport à l’objet O1 suspendu à l’un des deux côtés de la balance, à savoir 1° augmenter ou diminuer le poids de cet objet (action symbolisée par p ou par p) et 2° augmenter (= q) ou diminuer (= q) la distance L1 du poids par rapport à l’axe central de la balance (distance symbolisée par L2).
I = (p ∙ q) désigne l’opération d’augmenter à la fois le poids et la distance sur l’un des deux bras.
N = (p ∨ q) désigne les trois opérations possibles permettant d’annuler I, à savoir : (p ∙ q) ∨ (p ∙ q) ∨ (p · q), soit 1° conserver l’augmentation du poids, mais diminuer la distance, ou 2° diminuer le poids tout en conservant la distance, ou 3° diminuer le poids en même temps que la distance.
R et C concerne les deux types d’action possibles par rapport à l’objet O2 suspendu de l’autre côté de la balance, à savoir 1° augmenter ou diminuer le poids de ce deuxième objet (action symbolisée par p’ ou par p’ ) et 2° augmenter (= q’ ) ou diminuer (= q’ ) la distance du poids par rapport à l’axe central de la balance.
R = (p’ ∙ q’ ) soit non plus annuler mais compenser I en augmentant le poids et la distance L2 de O2 (donc du poids suspendu de l’autre côté du balancier). L’opération I d’augmenter le poids P1 et la distance L1 est compensée par l’opération R d’augmenter le poids P2 et la distance L2.
C = (p’ ∨ q’) désigne les trois opérations permettant d’annuler R, à savoir : (p’ ∙ q’ ) ∨ (p’ ∙ q’) ∨ (p’ ∙ q’). Chacune de ces trois possibilités agit dans le même sens que l’opération I, ce qu’exprime bien la notion de corrélation. Dès lors si l’on effectue I et que l’on effectue C sans effectuer l’opération R qui compensait l’action I, celle-ci se voit renforcée dans le cas où l’on diminue P2 et L2, mais aussi dans le cas (p’ ∙ q’) ou dans le cas (p’ ∙ q’), à condition bien sûr que l’une ou l’autre de ces deux dernières conjonctions d’action eût exactement compensé l’opération R si celle-ci avait été effectuée (sinon, bien que l’une des deux actions entreprises sur O2, par exemple q’, agisse dans le même sens que I, l’autre action p’, pourrait être suffisamment opposée à I pour que l’action conjointe, dans l’exemple (p’ ∙ q’), fasse pencher le balancier du côté de O2, la diminution de L2 ne suffisant pas à compenser l’augmentation exagérée du poids de O2).
Cela étant, examinons donc maintenant la progression des conduites des sujets confrontés à ce problème dont on va le voir qu’elle conforte la thèse de Piaget relative au rôle joué par les opérations formelles dans sa résolution.
Stade I (niveau préopératoire). — Entre 4 et 6 ans environ, les conduites observées se laissent répartir en deux sous-stades. Dans le premier des deux, les enfants n’ont aucune idée de l’action du poids ni du rôle de la distance sur les mouvements du balancier. Mic[25] (4;6), par exemple, place des poupées égales en poids, l’une à une distance de 14 cm, l’autre de 1 cm, en croyant qu’une fois cela fait, il suffit de mettre le balancier en position horizontale pour qu’il le reste (la notion d’horizontalité n’existant pas encore à ce niveau, l’expérimentateur montre par un geste la position dans laquelle le balancier devrait être). Constatant qu’après l’avoir mis dans cette position, le balancier, une fois lâcher, s’incline à nouveau, Mic affirme que l’ « on ne peut pas » (faire pour qu’il reste en position horizontale). Un autre enfant, Mar (4;8), pour atteindre l’objectif fixé, commence même jusqu’à suspendre deux poupées du même côté du balancier !
Par contre, lors du deuxième sous-stade, c’est-à-dire entre 5 et 7 ans environ, les sujets ont suffisamment joué avec des balances ou balançoires pour avoir acquis une certaine intuition du rôle qu’y joue le poids des objets. Ainsi Mal[26] (5;8), constatant qu’une poupée qu’il vient de fixer déséquilibre le balancier affirmera aussitôt qu’ « Il faut en mettre une (autre poupée) de l’autre côté. Je sais ce qu’il faudra faire : mettre de nouveau une autre là, parce qu’on n’a pas le poids d’ici » ; et comme elle constate que cette autre poupée une fois suspendue ne suffit pas à faire revenir le balancier en position horizontale, elle jugera même que celle-ci étant plus légère, « il faut prendre deux qui ont le même poids ». Elle découvre même, en cours d’expérience, que la distance à laquelle on place chacun des poupées joue un rôle. Ces enfants pourront donc parvenir face à chaque nouvelle situation à trouver en général une solution approximativement correcte, mais seulement par régulations ou tâtonnements successifs. Ils ne parviendront cependant pas à trouver le moyen de résoudre systématiquement et par anticipation opératoire le problème de poser sur le deuxième bras de la balance tel ou tel deuxième objet à telle ou telle distance, lorsqu’un premier objet est suspendu à telle ou telle distance sur le premier bras. Ils ne parviendront d’ailleurs pas non plus à établir des correspondances systématiques entre le poids et la distance, donc à saisir que « plus loin = plus lourd », contrairement à ce que l’on observe chez les sujets du niveau des opérations concrètes, qui sont capables de composer des sériations de poids avec des sériations (inverses) de distance.
Stade II (niveau des opérations concrètes). — Là aussi on distingue deux sous-stades. Dans le premier des deux, vers 7-9 ans environ, les enfants pressentent d’emblée, ou bien découvrent très vite que l’on peut résoudre le problème en s’efforçant de choisir des objets de même poids pour les placer à une égale distance de chaque côté du balancier, placer à une même distance un deuxième objet de même poids compensant ainsi l’action du premier objet placé sur le balancier. Ils devinent aussi ou découvrent que des objets de poids différents nécessitent de placer le deuxième objet à une distance différente, mais sans prévoir d’emblée la correspondance inverse entre poids et distances, ni une fois découverte en certaines situations cette correspondance inverse, la généraliser empiriquement à tous les cas.
Par exemple, Mas[27] (7;7) commence par prendre deux objets de poids approximativement égal pour les placer à une même distance. Suite à ce premier échec, il fait de même avec deux autres objets, et comme il aboutit de nouveau à un échec, il en soupèse deux autres en les plaçant à nouveau à égale distance, ce qui cette fois conduit à la réussite (sa démarche montrait qu’il cherchait d’emblée deux objets de même poids à placer à une même distance). Puis il explore plus avant les possibilités, en choisissant cette fois des objets de poids différents placés à des distances qu’il sait devoir être différentes, ce qui l’amène à une compensation empirique et par tâtonnement des poids et des distances, mais sans qu’il parvienne à dégager la loi « plus lourd » égal « moins loin » (ou moins lourd = plus loin) ce qui lui permettrait, en chaque nouvelle situation d’inégalité des poids, d’anticiper qu’un moindre poids peut être compensé par une distance plus grande, ou l’inverse.
Lors du deuxième sous-stade au contraire, dès 8-9 ans environ, les enfants qui ont découvert empiriquement cette loi de correspondance sériale inverse entre poids et distance cherchent systématiquement à mettre en correspondance inverse la distance du deuxième objet par rapport à celle du premier objet, en révélant ainsi qu’ils ont compris qu’un moindre poids peut être compensé par une distance plus grande, ou inversement. On a ici une démarche de compensation similaire à celles observées dans toutes les épreuves de conservation chez les sujets ayant atteint le niveau des opérations concrètes et qui, comme on l’a vu dans le cas de la conservation des liquides, justifient celle-ci en arguant du fait qu’une plus grande largeur (ou au contraire une hauteur plus grande) est compensée par une plus petite hauteur (ou largeur), un argument fondé, comme on l’a constaté, sur une correspondance inverse et une multiplication logique de deux séries de relations asymétriques.
Un exemple de comportements de ce deuxième sous-stade est livré par Fis[28] (10;7) qui constate qu’un premier objet O1 n’équilibre pas un autre objet déjà placé O2, et ceci, selon lui, parce que le premier « est plus lourd » alors que le second « est trop léger ». Pour parvenir à la solution, il faut donc « avancer » O1 du côté de l’axe. Fis croit que le fait de l’avoir « reculer de 16 trous » (nombre de trous intuitivement choisi), donc de l’avoir éloigné de l’extrémité du balancier près de laquelle O1 avait été fixé, a permis de baisser « de deux fois le poids ». Mais il ne peut préciser la raison de cette affirmation, se contentant d’observer que cette dernière a permis de faire que le poids P1 soit moindre (et donc que O1 soit monté). Sa conclusion est alors que quand on a deux poids différents, « on avance le plus lourd » du côté de l’axe de la balance. Mais Fis , tout en concevant donc une rapport de correspondance inverse entre poids et distance, est encore incapable d’établir un rapport de proportionnalité métrique inverse entre ces deux variables.
En définitive, comme dans les autres expériences mises en place pour étudier le fonctionnement de la pensée formelle, on constate qu’au niveau des opérations concrètes, les enfants font certes usage des possibilités d’organisation de l’expérience au moyen des opérations concrètes afin de trouver par essais et erreurs, et plus précisément par approximation progressive et anticipatrice la solution de chacun des problèmes auquel l’expérimentateur le confronte. Mais, faute de maîtriser opératoirement la notion de proportionnalité, ils ne peuvent pas, face à toute nouvelle situation, trouver directement, par anticipation déductive, la solution, ni même d’ailleurs être capable de la justifier après coup autrement qu’en recourant à la multiplication logique de deux sériations (« lorsque c’est plus loin, c’est plus lourd » et « là où c’est moins loin, c’est moins lourd »), opération acquise dès le niveau des opérations concrètes.
Stade III (niveau de la pensée formelle). — C’est à ce dernier niveau que les sujets découvrent la loi de proportionnalité qui régit l’équilibre de la balance. Par exemple, Tis[29] (13;8) ayant découvert la proportion 1 à 2 entre les poids de deux objets et dessiné les hauteurs correspondante, affirme : « Si je remplaçais ce poids (= O1) par celui-là (O2), ça ne monterait (à l’extrémité) que la moitié… ». A la question de savoir s’il y a compensation, il répond que « oui, entre la force et la hauteur » (comme sur une balançoire. Un autre sujet, Sam[30] (13;3), fait un raisonnement similaire pour un poids trois fois plus lourd. Il affirme qu’il « faut le mettre à 1/3 de la distance, ou faire en sorte que la hauteur de descente du plus léger soit égale à trois fois la hauteur de montée du plus lourd.
Chez ces sujets, il y a une claire intuition de la notion de travail (= force × distance). Plus une force (propre à un corps) est faible, plus la distance à parcourir pour équilibrer le travail d’un objet plus lourd doit être grande. Le poids d’un objet ne varie pas lorsqu’on déplace un corps sur le balancier. Seul le travail accompli par ce poids varie si on éloigne celui-ci de l’axe de la balance, et il diminue dans le cas contraire. Dès lors, si on augmente (ou diminue) n fois le poids, alors pour que son travail ne varie pas, il faut diminuer (ou augmenter) n fois sa distance (si l’on veut obtenir, ou conserver selon les situations, l’équilibre horizontal, et plus généralement telle ou telle inclinaison du balancier).
Les conditions de résolution opératoire du problème de l’équilibre de la balance. — Concluons cet examen de la progression de la pensée des enfants et des adolescents confrontés à des problèmes de proportionnalité tels que ceux qui interviennent dans le fonctionnement d’une balance en examinant de plus près les opérations logico-mathématiques utilisées par les sujets pour résoudre de manière pleinement opératoire ce problème qui paraît si trivial pour tout sujet parvenu au stade de la pensée formelle ou hypothético-déductive. En d’autres termes, pour quelle raison précise faut-il donc attendre ce stade pour que l’on voie les adolescents résoudre non plus par tâtonnements dirigés (c’est-à-dire par régulations empiriques certes orientées grâce aux opérations de la pensée concrète), mais par déduction et pleine anticipation opératoire ce problème ? Pour le comprendre, il faut revenir à la modélisation logique proposée par Piaget et que nous avons résumée plus haut.
Piaget explique cette apparition tardive par la nécessité de construire le système complet des compensations par inversion et réciprocité, en d’autres termes, et là encore, par la nécessité de maîtriser pratiquement le groupe INRC (ce qui ne veut pas dire en fournir la théorie, mais seulement d’être orienté dans ses actions, dans ses déductions et dans ses explications par cette maîtrise pratique des opérations du groupe INRC, ainsi d’ailleurs que d’autres opérations, par exemple combinatoires, qui toutes ensemble conditionnent la maîtrisent de la pensée hypothético-déductive, ou encore de la raison expérimentale et discursive). Selon Piaget, la clé de la solution réside dans la capacité des sujets de niveau formel de comprendre qu’ « augmenter le poids et la distance sur un bras de la balance [soit (p ∙ q)] est à l’augmentation symétrique sur l’autre bras [soit (p’ ∙ q’)] comme d’augmenter l’un ou l’autre sur un bras [soit (p ∨ q)] est à l’opération symétrique sur l’autre bras [soit (p’ ∨ q’)] »[31], soit :
Ce qui peut se ramener à la formule générale de la réciprocité en logique des propositions, qui signifie que pour toute opération propositionnelle, sa réciproque est la même opération, mais effectuée sur les propositions niées, soit, dans le cas particulier :
car : (p’ ∙ q’) étant la réaction symétrique, sur le deuxième bras, de l’action (p ∙ q) sur le premier bras, dont elle annule les effets, on a (p’ ∙ q’) = (p · q) de la formule précédente. C’est-à-dire que, comme on vient de le faire, on peut substituer (p · q) à (p’ ∙ q’) dans cette formule. Et il en va de même pour la partie droite de ces deux équations : comme la corrélative C = (p’ ∨ q’) de I = (p ∙ q) est la réaction symétrique (ou réciproque) de N = (p ∨ q) qu’elle annule (voir plus haut la définition de la corrélative), on peut également lui substituer (p ∨ q) dans la même formule (la réciproque de l’opération (p ∨ q) est la même opération effectuées sur les propositions niées, soit (p ∨ q)) ! En d’autres termes, l’opération réciproque R de I = (p ∙ q) peut aussi bien être réalisée par (p · q) que par (p’∙ q’), et l’opération corrélative C de I = (p ∙ q) peut aussi bien être réalisée par que par (p ∨ q) !
En conclusion, toute action I ou N faite à l’intérieur de l’un des deux sous-systèmes S1 qui intervient dans le problème de l’équilibre d’une balance peut non seulement être compensée 1° par son inverse ou sa réciproque à l’intérieur de ce même sous-système S1 (par exemple, si l’opération de départ est d’augmenter le poids de O en laissant invariante sa distance, on peut ou bien diminuer, par inversion, p, ou bien augmenter q (soit une réciprocité) pour compenser p), mais aussi 2° par une action symétrique faite dans l’autre sous-système = S2 (par exemple, si on augmente le poids et on diminue la distance dans S1, soit (p · q), on peux compenser en faisant (p’ · q’) dans S2, ce qui revient à annuler p (soit p) et à annuler la diminution q, soit à augmenter de q la distance dans S1 (ce qui annule tout, puisque –p+p=0 et –q+q=0)).
III. De la pensée concrète à la pensée formelle.
Conclusions générales
Le petit exercice auquel on vient de se livrer révèle que les opérations spontanées qu’effectue le sujet de niveau formel obéissent bien à une structure de groupe INRC qui agit sur différents plans et dont ce sujet ne sait pourtant rien ! En plus de révéler la structure cachée qui oriente la conduite et les justifications ou les raisonnements observés chez un tel sujet, l’intérêt d’une telle modélisation symbolique (laquelle emprunte ses outils à la logique interpropositionnelle analysée et modélisée par Piaget dans son Traité de logique de 1949) est de montrer l’identité de structure des opérations qui interviennent dans les multiples résolutions de problèmes auxquels ont été confrontés enfants et adolescents. Par là même, et au delà des cas particuliers livrés par les expériences exposées dans La genèse de l’idée de hasard et surtout dans De la logique de l’enfant à la logique de l’adolescent, c’est la pensée de l’adolescent (et plus généralement de la pensée commune que l’on devrait idéalement pouvoir observer chez tout adulte qui, adolescent, sera parvenu au stade de la pensée hypothético-déductive) dont les caractéristiques les plus profondes sont ainsi mises à jour à travers les travaux conjoints de Piaget et d’Inhelder.
Résumons donc pour terminer quelles sont ces caractéristiques que nous avons pu à notre tour cerner lors de ces deux cours consacrés à la dernière des grandes étapes de développement de la pensée commune (c’est-à-dire de la pensée qui, dans des contextes bien précis et sous certaines conditions devrait être observée chez tout être humain parvenu à sa pleine maturité).
La pensée formelle ou hypothético-déductive observée par Inhelder et Piaget dans leurs recherches sur la logique de l’adolescent présente quatre caractéristiques essentielles, dont la première est la plus manifeste : 1° le primat du possible sur le réel, 2° la capacité combinatoire, 3° l’accès aux opérations interpropositionnelles, 4° la présence de structures opératoires sous-jacentes guidant le sujet dans son approche expérimentale et sa compréhension du réel (structure de groupe INRC, mais aussi d’autres structures telles que celle de treillis ou d’ensemble partiellement ordonné [32], tout aussi importante et reliant l’ensemble des seize opérations de base de la logique des propositions : l’implication, la négation, la conjonction, la disjonction exclusive ou non exclusive, etc.).
En ce qui concerne le primat du possible sur le réel, il se révèle dans la capacité de l’adolescent non pas seulement d’imaginer des univers fictifs, comme le font les enfants plus jeunes qui (se) racontent des histoires, mais aussi et surtout de concevoir que le réel concret auquel il se confronte aurait pu être autre qu’il n’est, que d’autres réalités eussent été possibles pour autant que les conditions de départ qui ont conduit à l’état de choses observés dans telle situation eussent été différentes. Ce faisant, le positionnement de l’adolescent face au réel présent et à venir se modifie considérablement, dans la mesure où il peut concevoir qu’en changeant l’état actuel de certaines réalités, il peut rendre possible l’avènement de réalités à venir souhaitables (à ses yeux)[33] et dont l’existence, sans ces modifications actuelles, resterait sinon impossible du moins peu probable. Ce changement d’attitude face au monde, ce basculement entre le possible et le réel qui fait de ce dernier une simple actualisation d’un ensemble certes largement indéterminé de possibles est la marque la plus visible de la pensée adolescente. Or ce changement, d’où provient-il, sinon de la transformation profonde que subit la pensée logique à partir de 10-12 ans environ, c’est-à-dire de la construction d’un ensemble d’opérations logiques de second degré, qui agissent sur les compositions d’opérations concrètes préalablement acquises chez l’enfant entre 6-7 et 10 ans environ. Les opérations concrètes ont pour particularité d’organiser et d’expliquer le réel actuel [34] en comparant, en classant, en ordonnant (notamment dans l’espace et dans le temps), en énumérant ou encore en mesurant les objets ou les événements qui s’y déroulent. La réalité à laquelle se confronte l’enfant est d’ailleurs encore cette réalité que l’adolescent et nous-mêmes adultes continuons à percevoir et à nous représenter dans la vie de tous les jours, au moyen des mêmes opérations logico-mathématiques concrètes que nous avons construites au cours de notre enfance et dont on a vu dans les précédents cours qu’elles sont regroupées en structures obéissant à des règles de composition bien déterminées. Mais ces opérations concrètes, ou plutôt les structures qu’elles composent et qui orientent leur fonctionnement, sont lacunaires, notamment face à la complexité d’un réel qu’elles ne parviennent pas à démêler, à organiser et à expliquer, ou encore face à la diversité des conceptions et des explications contradictoires que les différents sujets peuvent élaborer à son égard. En cherchant à rendre plus saisissable, plus assimilable ce réel, en cherchant à démontrer et à justifier les explications qu’il en donne, le sujet parvient à prendre une certaine distance par rapport à ses opérations concrètes, à les penser et les organiser de manière réfléchie pour qu’elles puissent à leur tour mieux organiser le réel concret sur lequel elles agissent. De cette recherche d’une compréhension et d’une capacité d’action supérieures naissent de nouvelles opérations, dont certaines au moins proviennent de l’application réflexive des opérations de classification et de sériation aux opérations concrètes elles-mêmes : sérier des sériations et des classifications, classer des classifications et des sériations, mettre en correspondance des systèmes ou des regroupements opératoires fonctionnant d’abord, sur le plan de la pensée concrète, soit de manière isolées, soit pêle-mêle, sans ordre, sans conduite organisatrice. C’est donc de ce besoin fonctionnel de dépasser les limitations de la pensée concrète, et de la possibilité d’utiliser les opérations concrètes pour organiser non plus seulement le réel, mais, sur un plan plus abstrait, les opérations concrètes de la pensée elle-même, que naissent des opérations formelles, des opérations qui agissent non plus sur un plan prioritairement concret, mais sur le plan hypothético-déductif des possibles. Ceci nous conduit à ces autres caractéristiques de la pensée formelle, c’est-à-dire à ces opérations et ces structures nouvelles sans lesquelles ce besoin ne trouverait pas satisfaction.
En ce qui concerne ces autres caractéristiques, nous pouvons être plus bref, puisque ce sont elles qui ont été l’objet central de nos deux cours sur la pensée de l’adolescent.
Les exemples présentés ont montré que la pensée combinatoire agit au moins sur deux plans reliés l’un à l’autre, ou même se conditionnant mutuellement : 1° celui des objets du monde extérieur, réel ou virtuel, ou encore celui de leurs représentants symboliques (c’est le cas de cet adolescent interrogé dans le cadre des recherches de B. Inhelder sur le raisonnement inductif —voir note 18— qui, muni d’une feuille et d’un crayon, liste de manière symbolique l’ensemble des combinaisons possibles de différentes substances chimiques dont le mélange peut conduire à faire surgir des phénomènes attendus ou inattendus) ; 2° celui des propositions logiques, exprimées ou non, au moyen desquelles le sujet conçoit la réalité présente ou, plus abstraitement, un ensemble de possibilités. Ces deux plans sur lesquels agit la pensée combinatoire se conditionnent mutuellement en ce sens que la pensée adolescente, tout en renversant le rapport existant entre le possible et le réel (celui-ci n’étant plus considéré que comme une actualisation de l’un des possibles concevables) ne cesse pas pour autant d’avoir toujours en vue non pas des symboles logiques dépourvu de toute signification, mais des symboles, et en tout premier lieu des énoncés verbaux, des propositions logiques portant toujours ou presque sur des réalités actuelles ou possibles ; et qu’inversement, le rapport concret du sujet à ces réalités réelles ou possibles est toujours médiatisé par l’usage de la pensée propositionnelle, que les propositions au moyen desquelles sont assimilées ces réalités soient explicitement formulées ou, restant non formulées, qu’elles échappent à l’attention du sujet pensant ce réel et même agissant sur lui. Rappelons enfin comment les opérations combinatoires interviennent sur ces deux plans de l’action organisatrice du réel et de la pensée propositionnelle. Sur le premier plan, on les voit à l’œuvre lorsque le sujet ayant atteint le stade de la pensée formelle parvient sans problème, après quelques tâtonnements, à réunir de toutes les manières possibles les éléments d’un ensemble d’objets pouvant être combinés les uns avec les autres. Sur le second plan, ce sont cette fois des combinaisons de propositions logiques qu’il s’agit de composer dans le but de formuler des hypothèses et d’attester expérimentalement ou par voie exclusivement déductive leur valeur de vérité ou de fausseté, que ce soit pour découvrir les causes d’un phénomène, et ainsi se convaincre soi-même ou autrui de la valeur des jugements portés sur telle ou telle réalité (se prouver par exemple à soi-même et à autrui que c’est exclusivement la longueur d’un pendule et non pas son poids qui explique la fréquence de ses battements), ou que ce soit, si l’on a une âme de théoricien, pour se convaincre ou convaincre autrui de la justesse d’une thèse ou même d’un théorème.
Bien entendu, dans la vie de tous les jours, il est rare de se trouver dans une situation dans laquelle la pensée formelle peut déployer toute sa puissance organisatrice et transformatrice du réel, ainsi que sa puissance démonstrative. Mais il n’en demeure pas moins que l’adolescent qui a atteint le stade de la pensée hypothético-déductive et se trouvant dans la situation où il s’agit de se convaincre ou de convaincre autrui de la justesse de ses thèses, ou bien dans la situation où il cherche à découvrir toutes les combinaisons possibles d’un ensemble d’éléments, ou à comprendre un phénomène, ne manquera pas d’utiliser les instruments intellectuels dont il dispose et donc de recourir à ces opérations que les recherches d’Inhelder et de Piaget ont mis en lumière au début des années 1950.
Enfin, dernière caractéristique de la pensée adolescente : la présence sous-jacente de structures organisant et réglant les compositions d’opérations combinatoires et interpropositionnelles lorsque la pensée procède par déduction aussi bien dans ses conduites face au réel que dans les raisonnements par lesquels le sujet cherche à attester la vérité ou la fausseté de telle ou telle thèse, ou encore à construire une conception logiquement cohérente de telle ou telle réalité. La présence de ces structures est essentielle en ce sens que, tant qu’elles ne sont pas pleinement acquises, c’est-à-dire tant que les opérations sur lesquelles elles portent ne sont pas pleinement composées les unes avec les autres par des opérations propres à ces structures (par exemple les opérations du groupe INRC), les capacités déductives de la pensée formelle en formation n’atteignent pas leur pleine puissance, le recours à une démarche empirique procédant par tâtonnement dirigé par des intuitions et déductions incomplètes restant alors nécessaire pour atteindre les buts que se fixe le sujet (ou qu’autrui lui suggère).
En définitive, tout l’apport de Piaget et d’Inhelder concernant le développement de la pensée formelle prolonge et complète ce que les travaux de psychologie génétique antérieurs étaient parvenus à mettre en lumière concernant la pensée de l’enfant, qui elle aussi n’atteint sa pleine puissance fonctionnelle qu’une fois regroupées les préopérations concrètes au moyen desquelles le jeune enfant organisait et pensait les réalités qui étaient les siennes — et ceci de la même façon que cette mise en lumière, dans les années 1930-40, des structures sous-tendant le fonctionnement de la pensée concrète prolongeait et complétait ce que les travaux encore plus anciens de psychologie génétique avait révélé, dans les années 1920-1930, concernant le fonctionnement de l’intelligence sensori-motrice, qui elle aussi n’atteignait son équilibre que grâce à la composition de groupes d’actions tels que celui des déplacements des objets (et du corps propre) dans l’espace plus ou moins proche environnant le bébé. A chaque fois ce sont des étapes similaires que l’on observe dans le développement successif de ces trois plans de l’intelligence sensori-motrice, de l’intelligence concrète et de l’intelligence formelle : une première étape où les éléments composant ces trois formes d’intelligence fonctionnent de manière dispersée et peu organisée, puis une étape intermédiaire lors de laquelle sont introduites des liaisons empiriquement ou intuitivement fondées entre ces éléments, enfin une étape finale lors desquels l’ensemble des liaisons entre éléments est assuré par la présence de ces structures sous-jacentes, c’est-à-dire fonctionnellement actives mais dont le sujet n’a pas conscience ou dont la prise de conscience se limite aux sentiments de cohérence et de nécessité logique qui reflètent leur stabilité intrinsèque.
Avec ces deux cours sur la pensée formelle se termine la présentation des recherches de Piaget et de ses plus proches collaborateurs et collaboratrices sur le développement de l’intelligence sensori-motrice puis de l’intelligence représentative et notionnelle, du bébé jusqu’à l’adolescence. Comme j’ai eu plusieurs fois l’occasion de le souligner, ces recherches n’avaient pas seulement pour but de mieux saisir le développement de l’intelligence et de la raison humaine, mais également d’apporter des informations essentielles à l’essor de cette épistémologie génétique dont Piaget avait posé les premiers jalons dès les années 1920. La semaine prochaine, je reviendrai sur les buts fixés au début de ce cours sur l’œuvre de Piaget et de son rapport à la psychologie du développement, ce qui me conduira à récapituler à grands traits ce que j’ai eu l’occasion de présenter lors de ce semestre, mais aussi à exposer de manière inévitablement lacunaire quelques aspects ou chapitres de l’œuvre que je n’ai pas eu le temps d’aborder.
_____________________
[1] N’oublions pas la remarque faite à propos des stades de la naissance de l’intelligence sensori-motrice chez l’enfant, remarque généralisable à tous les niveaux de pensée. Dans le cas particulier le fait qu’un sujet atteigne un nouveau stade n+1 de développement n’implique en rien que ses anciens schèmes de niveau n–k n’interviennent plus dans ses conduites et dans sa manière de percevoir ou de concevoir le réel dans ses rapports avec le possible. Arrivé au stade formel, ce n’est même généralement que dans des conditions particulières que le sujet sera amené à faire usage de ses compétences de ce niveau.
[2] J. Piaget et B. Inhelder, La genèse de l’idée de hasard chez l’enfant, PUF, 1951.
[3] Rappelons que les âges indiqués doivent être pris avec précaution. Selon les sociétés et les types d’éducation, ces âges peuvent être décalés de une année ou deux voire davantage.
[4] La genèse de l’idée de hasard, p. 176.
[5] L’ensemble des couples de couleurs différentes est composé du tableau cartésien de tous les couples possibles, auxquels on soustrait la diagonale du tableau qui représentent les couples monocolores, le résultat de cette soustraction étant ensuite divisé par 2, dans la mesure où l’ordre de couleurs dans un couple n’est pas pertinent (par exemple, R,Bc ne se distingue pas de BcR).
[6] Op. cit., p. 179. Le protocole complet des réponses de cet enfant se trouve dans le chapitre 7 de ouvrage La genèse de l’idée de hasard chez l’enfant. Ce chapitre est disponible sur le site de la Fondation Jean Piaget. [*]
[7] Id., p. 180.
[8] Id., p. 183.
[9] B. Inhelder et J. Piaget, De la logique de l’enfant à la logique de l’adolescent. Paris : PUF, 1955, pp. 97-109.
[10] Voir Cours 10, note 25, la définition donnée par Piaget d’une explication de type phénoméniste.
[11] Pour un aperçu des différentes sortes de causalité prélogiques (donc propres aux enfants de niveau préopératoire), voir les chapitres de La causalité physique chez l’enfant (ouvrage de J. Piaget publié en 1927) placés sur la page suivante du site de la Fondation Jean Piaget (sous l’année 1927) [*].
[12] Inhelder et Piaget, 1955, p. 99.
[13] Un extrait de film réalisé dans le cadre des recherches longitudinales de B. Inhelder et de ses collaborateurs sur le raisonnement chez l’enfant et l’adolescent illustre des comportements typiques d’enfants de ce niveau confrontés à ce problème de combinaison des liquides.
[14] Voir De la logique de l’enfant à la logique de l’adolescent, p. 100.
[15] Id., p. 103.
[16] Id., p. 103.
[17] Il est important de noter que les enfants et adolescents interrogés n’ont jamais eu l’occasion d’apprendre les opérations combinatoires dans le cadre de leur cursus scolaire. Ces opérations, ils les acquièrent progressivement en opérant sur dans des situations lors desquelles il s’agit de combiner des éléments variés.
[18] Un extrait de film réalisé par B. Inhelder et ses collaborateurs dans les années 1950 permet là aussi d’apprécier le progrès que permet la maîtrise de la pensée (et des opérations) combinatoires par rapport à la seule maîtrise des opérations concrètes, face à un problème de combinaison des corps chimiques.
[19] C’est dès ses premiers travaux réalisés dans les années 1920 que Piaget avait découvert l’existence de ces deux paliers de l’intelligence opératoire que sont la pensée concrète puis la pensée formelle. Mais ce n’est pas avant la fin des années trente (pour les opérations concrètes) et la fin des années quarante (pour la pensée formelle) qu’il découvrira les structures que composent respectivement les opérations concrètes et les opérations formelles.
[20] Les notions de mouvement et de vitesse chez l’enfant, 1946, p. 97.
[21] L’enfant sait quel est le point de départ de la planche et de l’escargot avant leur mouvement (une marque est laissée sur la table sur laquelle la planche est déplacée, cette marque correspondant chaque fois à l’extrémité de la planche où se trouve l’escargot au départ de leurs mouvements respectifs, soit de même sens, soit de sens contraire). Par ailleurs, au départ de l’expérience, et pour justifier les mouvements qui seront effectués avec la planche, l’expérimentateur indique aux enfants interrogés que ces mouvements sont effectués pour « faire des farces » à l’escargot. Les sujets ont également à disposition des bandelettes de papier pour leur permettre de juger la longueur des déplacements réalisés soit par l’escargot, soit par la planche, soit par l’un et l’autre.
[22] Id., p. 98.
[23] Piaget, Les notions de mouvement et de vitesse chez l’enfant, 1946, p. 108. Le chapitre 5 de cet ouvrage dans lequel est reportée cette expérience sur l’acquisition des composition des mouvements relatifs chez l’enfant est disponible sur le site de la Fondation Jean Piaget (sous Textes/extraits, année 1946 [*]).
[24] Je ne détaille pas complètement la formalisation ébauchée par JP (cette formalisation, qui contient de petites erreurs, est présentée p. 155-158 de l’ouvrage De la logique de l’enfant à la logique de l’adolescent (chapitre 11). Une version électronique révisée de ce chapitre est disponible sur le site de la Fondation Jean Piaget (sous Textes/extraits, année 1955 [*].
[25] Voir De la logique de l’enfant à la logique de l’adolescent, p. 145.
[26] Id., p. 146. Un extrait de film réalisé par B. Inhelder et ses collaborateurs dans les années 1950 illustre également le type de comportement observé à ce sous-stade chez une fillette de 6 ans et 1 mois.
[27] Id., p. 147-8.
[28] Id., p. 149. Un extrait de film réalisé par B. Inhelder et ses collaborateurs dans les années 1950 illustre également le type de comportements que peut voir à l’œuvre chez un enfant de 9 ans et 8 mois maîtrisant l’opération de multiplication logique de deux relations asymétriques dans le cadre de ce problème d’équilibre de la balance.
[29] Id., p. 152.
[30] Id.
[31] Id., p. 156.
[32] En mathématiques, une structure de treillis caractérise tout ensemble partiellement ou complètement ordonné, dans lequel chaque couple d’éléments admet une borne supérieure et une borne inférieure (en logique des propositions, pour prendre un exemple très simple, la borne supérieure de la conjonction (p ∙ q) et de la disjonction (p ∨ q) est (p ∨ q) et la borne inférieure (p ∙ q).
[33] Dans leurs conclusions générales dans lesquelles Inhelder et Piaget décrivent les grands traits de la pensée adolescente, ils ne manquent pas de souligner que si l’accès à la pensée hypothético-déductive permet à l’adolescent de prendre quelques distances par rapport au réel actuel et ouvre largement l’horizon des possibles, elle ne s’en accompagne pas moins d’une nouvelle forme d’égocentrisme (et de sociocentrisme) qui n’est certes plus celle de la petite enfance et que la pensée opératoire concrète a su dépasser, mais qui reproduit sur le nouveau plan des possibles une déformation des perspectives rendant ceux-ci largement illusoires et par trop centrés sur les certitudes et les désirs personnels ou du groupe des pairs dont il se sent membre.
[34] La notion d’actuel doit bien sûr être entendue en son sens le plus large, qui inclut non seulement l’horizon des tâches ou activités quotidiennes, ainsi que des objets et des personnes qui leur sont liées, mais les événements mémorisés du passé, ainsi que les activités qui devraient se dérouler dans le futur (vacances à venir, fêtes d’anniversaire et mille autres événements attendus).